Multiplying fractions is easy. However, many are asking how to multiply fractions.
To begin with, we do not need to worry about what kind of fractions we are dealing with, whether similar or dissimilar.
Likewise, we do not need to find the least common denominator.
Above all, the only thing we need to consider is that our fractions must not be in a mixed form to avoid confusion.
How to Multiply Fractions – Step-by-step
To start with, I have enumerated below the step-by-step procedure for how to multiply fractions:
Step 1. First, check the fractions and their operation. Initially, check the multiplication sign or symbol. Then, if the fraction is in mixed form, convert the fraction into improper fractions.
Step 2. Next, multiply their numerators.
Step 3. Then, multiply their denominators.
Step 4. Finally, convert your answer to its lowest term. Similarly, write your answer into a mixed number if required.
How to Multiply Fractions – Clear Examples
Example no. 1
As our first example, we will multiply both proper fractions. For instance, let’s multiply 2/3 and 3/4.

Additionally, follow this link if you want to review simplifying fractions.
Example no. 2
Now, let’s try multiplying a proper fraction to an improper fraction. For example, solve 4/6 x 5/2.

For converting an improper fraction into a mixed number, follow the related post in this link.
Example no. 3
Next, let’s try another example. Again, we are going to multiply improper fractions. For instance, solve 5/4 x 8/3.

Example no. 4
Moving on, we can also multiply a fraction and a whole number. For example, try 1/2 x 100.
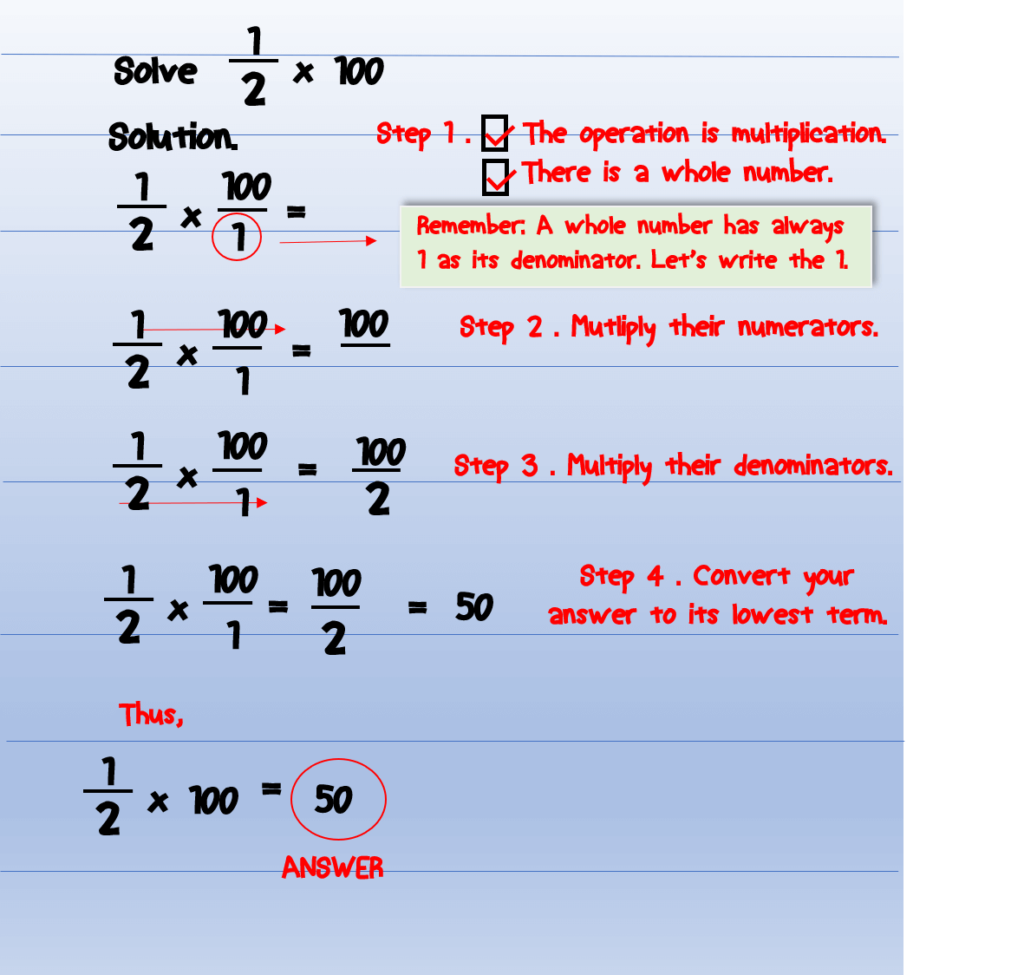
Example no. 5
To put it another way, what if the whole number is our dividend? For example, let’s see by finding the product of 20 and 3/4.

Example no. 6
Moreover, what about multiplying fractions that involve a mixed form fraction? For illustration, let’s solve 1/2 x 3 1/3.

Example no. 7
To understand further, let’s take a look at this example. Solve 4 2/3 x 5/8.

Example no. 8
To put it differently, let’s multiply a whole number to a mixed number in this example. For example, solve 2 x 3 3/7.

Example no. 9 For our last example, let’s solve 2 2/7 x 3.

Meanwhile, have you noticed that our previous example has the same result as our last example? Hence, this saved me some time to edit the illustrations.
Summary
Most importantly, to multiply fractions, you must know at least the following:
- Of course, you must know how to perform basic multiplication.
- Then, you must understand what is proper fractions, improper fractions, and mixed numbers.
- Finally, you must know how to simplify fractions.
Related Topics
Please write your comments, suggestions, or questions in the comment box below if you find this blog interesting. I am happy to hear from you guys.

Thanks.
You’re welcome.