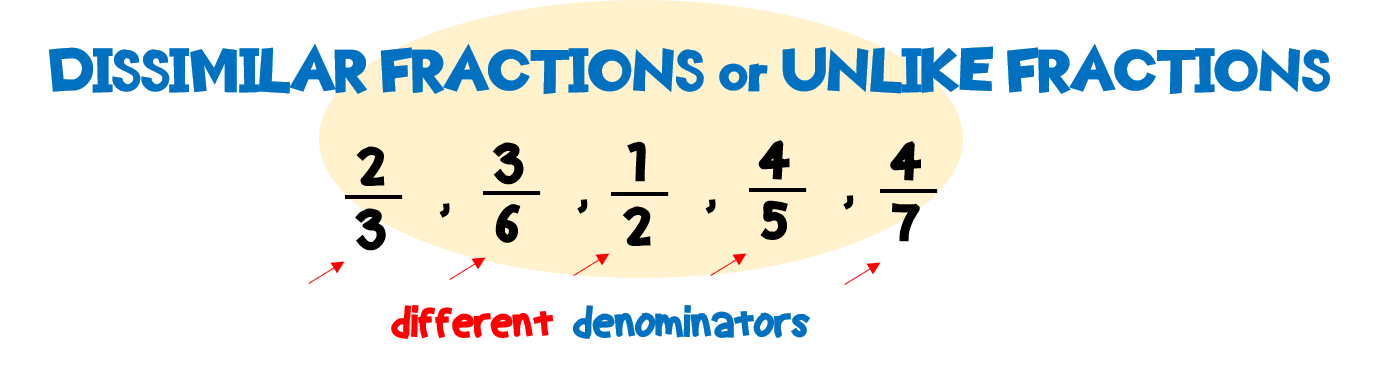
Okay. Here’s the thing. The addition or subtraction of dissimilar fractions (unlike fractions) is slightly different compared to the addition or subtraction of similar fractions (like fractions).
For the addition or subtraction of similar fractions, we are dealing only with the numerators. If you missed my previous lesson, you could review my previous discussion about the addition and subtraction of similar fractions.
Meanwhile, for the addition or subtraction of dissimilar fractions, it means that we will be dealing both with numerators and denominators.
For you to proceed with this lesson easily, please make sure that you have a full understanding of the following topics:
1. Addition and subtraction of similar fractions (or like fractions).
2. Finding equivalent fractions.
3. Finding the “Least Common Denominator” or LCD.
Let’s start with the basic steps.
How to Add Unlike Fractions (dissimilar fractions) Step-by-step.
To make it easy, I divided the procedure on how to add or subtract unlike fractions into two (2) basic steps as follows:
Step 1. Change all unlike fractions (dissimilar fractions) into like fractions (similar fractions).
In order to this, we need to change the denominators of the fractions into a common denominator. Remember that similar fractions has the same or common or like denominators.
The common denominator must be a multiple of all different denominators. Meaning to say, the common denominator can be divided by all the denominators without any remainder.
There are infinite numbers of common denominator for any fractions, but we will consider only the smallest or the lowest one. This is what do we called the least common denominator or LCD.
Finally, obtain the equivalent fractions of those fractions using the common denominator obtained.

Step 2. Proceed with the same procedure as adding or subtracting similar fractions.
We will follow the same procedure of adding or subtracting similar fractions as follows:
- Add or subtract the numerators.
- Copy the denominators.
- Convert the final answer in the lowest term.
Let us have an example.
Adding Unlike Fractions – Examples
Example No.1 Find the sum of 1/4 and 1/2.

First step is to find the least common denominator of 1/4 and 1/2. It is the same as finding the least common multiple of 4 and 2.
Our least common denominator is 4 as shown above. The next to do next is to put 4 as our new denominators.
Then, we will find the equivalent fractions of our original fractions with 4 as the denominator.
1/4 will not change. 4 is already the denominator.
The equivalent fraction of 1/2 with 4 as the denominator is 2/4.
Now, we have 1/4 plus 2/4. We can easily add this now because they are similar fractions.
1/4 plus 2/4 is equal to 3/4. We just simply add the numerators.
Since our sum which is equal to 3/4 is already in the lowest term, 3/4 is the final answer.
Example No.2 Find the sum of 2/3 and 1/4.

The first thing that we want to do is to change those fractions into similar fractions.
In order to do that, we must find the LCD. The LCD is the least common multiple of 3 and 4.
In our solving above, the least common multiple of 3 and 4 is 12. We will use 12 as our new denominator.
The next thing to do is to find the equivalent fraction of 2/3 and 1/4 with 12 as the denominator.
The equivalent fraction of 2/3 with 12 as the denominator is 8/12.
The equivalent fraction of 1/4 with 12 as the denominator is 3/12.
Since we have already changed them into similar fractions, we can proceed with adding their numerators.
8/12 plus 3/12 is equal to 11/12.
11/12 is our answer.
More example of adding unlike fractions.
Example No.3 Find the sum of 1/6 and 3/4.

Example No.4 Find the sum of 4/5 and 3/4.

Example No.5 Find the sum of 1/6, 2/9, and 5/18.

How to Subtract Unlike Fractions (dissimilar fractions) – Steps
First, we will change dissimilar fractions into similar fractions by finding the least common denominator.
Second, add them like similar fractions.
And then finally, convert the answer in the lowest term.
Subtracting Unlike Fractions – Examples
Example No.6 Subtract 3/4 from 4/5.

What will be our least common denominator? The least common multiple of 5 and 4 is 20. Thus, 20 is our least common denominator.
The equivalent fraction of 4/5 with 20 as the denominator is 16/20.
The equivalent fraction of 3/4 with 20 as the denominator is 15/20.
Since we already have similar fractions, perform the subtraction.
16/20 minus 15/20 is equal to 1/20.
1/20 is in the lowest term.
Thus, 1/20 is the final answer.
Example No.7 Subtract 1/4 from 2/3.

First, solve for the least common denominator. The least common denominator is 12 as shown in our calculation.
The equivalent fraction of 2/3 with 12 as the denominator is 8/12.
While the equivalent fraction of 1/4 with 12 as the denominator is 3/12.
Thus, 8/12 minus 3/12 is equal to 5/12.
5/12 is already in the lowest term.
Thus, 1/20 is the final answer.
Summary – Adding and Subtracting Unlike Fractions
- To add or subtract dissimilar fractions (or unlike fractions), change dissimilar fractions into similar fractions (or like fractions). Then, add or subtract the fractions as similar fractions. The sum or difference must in the lowest term.
- To change dissimilar fractions (or unlike fractions) into similar fractions (or like fractions0, we need to find the Least Common Denominator or LCD.
Related Topics
1. Addition of Similar Fractions.
2. Subtraction of Similar Fractions.
4. What are dissimilar fractions or unlike fractions?
5. What are similar fractions or like fractions?
7.What are equivalent fractions?
If you have some questions or problems related to the above topic, please feel free to drop it in the comments section below.
Please do not forget to share this post with your friends, classmates, brothers, sisters, or siblings.
Enjoy!

I like the way you patiently explained every step that it is easily understandable to a child. I think parents will love this site. I am just seeing it for the first time. As a child, I wasn’t too good at math but then we didn’t have access to materials like this and patient teachers such as you. Or maybe we did have good teachers but were too resigned to follow what they taught.
Thank you Chyke. I really appreciate it. I love teaching kids and I love sharing my math knowledge to them.
Your explanation was very organized and systematic. Honestly, I was never much of a math wiz, but your use of pictures was very effective. The steps were also extremely clear. Great job!
Thank you. I love teaching. Please come back for more my interesting posts.
As a father , I am teaching my daughter simple and basic maths and seeing your website and how you have painstakingly analysed every step that it is easily understandable to a child.
I am bookmarking your blog because I can learn more and transfer the skills to my girls. I use Kumon to teach them at the moment but when it comes to the logic I need to delve deeper just like you have done.
Growing up I loved maths and further maths but now into construction but not lost my love for the subject.
Thanks
Exactly. This is actually one my purpose – to help parents or kids to understand basic math topic better.
Regards.
This was actually a really well thought out lesson, thank you for that! I was always decent with math in school so this was nothing new really but I can’t actually remember that we would have learned to find the LCD the way you showed here. It’s really simple and logical and I actually learned something new :).
You’re welcome. I tried to present all the lessons in its most basic approach.
This post contains a very detailed explanation in adding and subtracting fractions. It present an effective method on finding the LCD. I could say this is very helpful to pupils who just started learning fractions. I also want to share my idea on dealing with fractions but I think this is suitable for higher grade levels.
To add and subtract fractions successfully is to make the rules stick to your memory.
Rules are:
Same denominator:
Add both numerators then reduce. The result would be the final answer.
Different denominator (4 steps):
1. Multiply the numerator of first fraction to the denominator of second fraction. The result is the new numerator of first fraction.
2. Multiply the numerator of the second fraction to the denominator of first fraction. The result is the new numerator of second fraction.
3. Multiply both denominators. The result is the common denominator for two fractions.
4. Add the two new numerators. The result is the answer.
To make it stick to your memory:
Rules for subtraction:
Same denominator:
Subtract second numerator from first then reduce. The result would be the final answer.
Different denominator (4 steps):
1. Multiply the numerator of first fraction to the denominator of second fraction. The result is the new numerator of first fraction.
2. Multiply the numerator of the second fraction to the denominator of first fraction. The result is the new numerator of second fraction.
3. Multiply both denominators. The result is the common denominator for two fractions.
4. Subtract new second numerator from first new numerator. The result is now the answer.
To make it stick to your memory:
Same numerator:
Add two fractions 50 times.
Subtract two fractions 50 times.
Different denominator:
Add two fractions 100 times.
Subtract two fractions 100 times.
To check if your answer is right and your step by step solution is correct:
Use fraction calculator with button from http://www.fractioncalc.com. It is important that you follow the correct steps in adding unlike fraction. Unlike fractions are those fractions with different denominator.
The key here is to make the rules implanted into the minds of the students so that they will never forget.
I am very very happy with this website.
Tanks.
I love youur blog.. very nicxe colors & theme. Did youu make this website yourself oor did you hire someone to do it for
you? Plz respond as I’m looking to construct my own blog and would like to find out where u got this from.
thanks
Yes. I make my own blog. I pay from a webhosting provider.
Hi there, I enjoy reading all of your article post. I wanted to
write a little comment to support you.
Thank you.