Logarithms can seem intimidating at first, but once the core rules click, math gets a whole lot easier. Whenever I’m solving exponential equations or need to simplify something, understanding the basic log rules saves tons of time and confusion.
You might run into logarithms in algebra, science, engineering, finance, or just about any field with exponential growth or decay. Whether you’re new to logs or brushing up after a break, getting comfortable with how their rules work is time well spent. I’ll walk you through the main rules, explain why they matter, and show some go-to tips for making problems less of a headache.
This guide covers the classic log rules step by step, with real examples and my own take on how I like to remember each bit. If you ever felt unsure about parentheses or got tangled up in base changes, you’ll find explanations that make things clear without math jargon overload.
The Basics: What Logarithms Mean
A logarithm answers the question: “To what power do I raise the base to get a certain number?” If you see log10 100, you’re just looking for the exponent that turns 10 into 100, which is 2. In simple terms, log10 100 = 2 because 102 = 100.
Common Notation
- log x usually means base 10. (Common logarithm)
- ln x means base e, about 2.718. (Natural logarithm)
- logb x is the log with base b, whatever number b is.
Understanding the basics helps every rule make more sense later.
Product, Quotient, and Power Rules
The main rules for logarithms let you split up or combine tricky expressions. Each one comes from basic exponent ideas, just flipped around for logs.
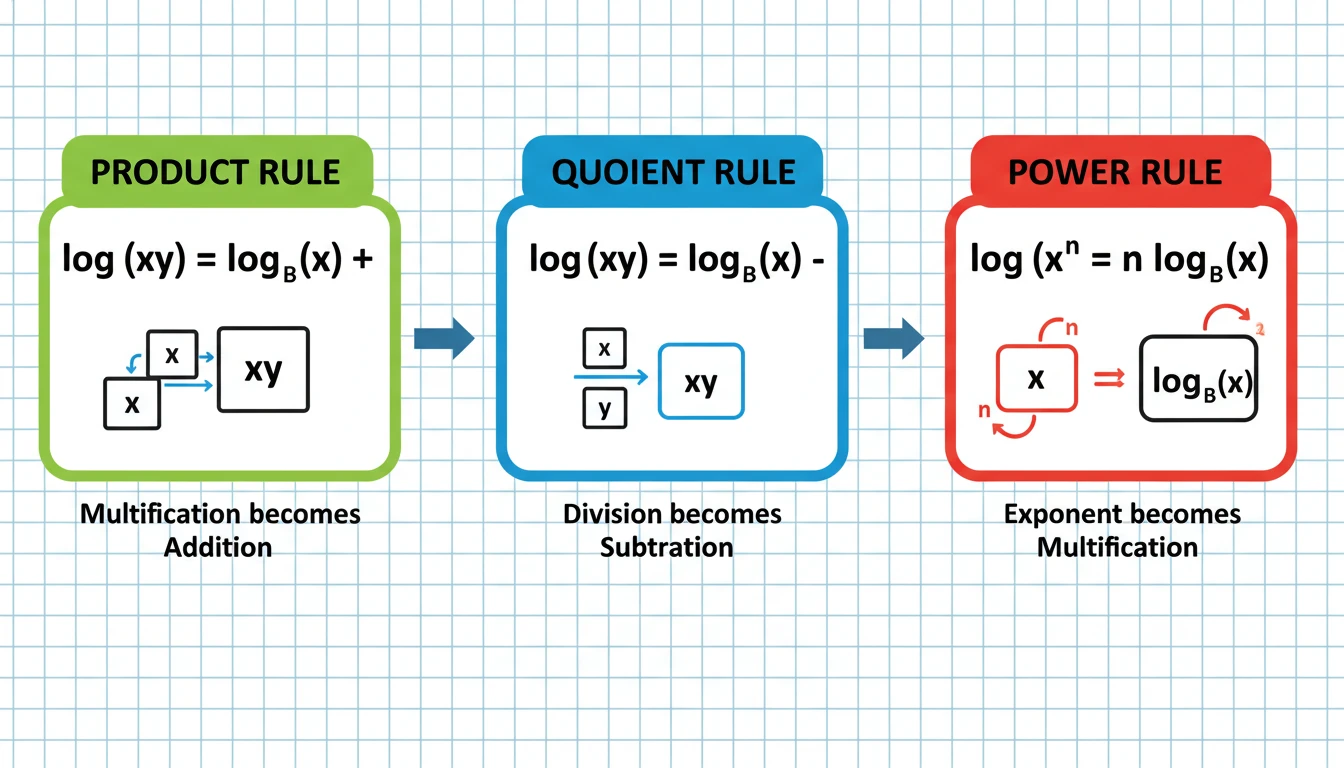
Product Rule
logb(MN) = logb M + logb N
This lets you turn multiplication inside a log into addition outside. Honestly, I use this the most when breaking down big numbers or untangling log equations.
Example:
log10 (1000 × 10)
= log10 1000 + log10 10
= 3 + 1
= 4
Quotient Rule
logb (M/N) = logb M − logb N
Division in a log turns into subtraction. If you see a fraction inside, try rewriting it with this rule so your life is easier.
Example:
log2 (32 / 4)
= log2 32 − log2 4
= 5 − 2
= 3
Power Rule
logb (Mp) = p × logb M
This rule is really helpful whenever an exponent hangs around inside a log. You just pull the exponent down in front, and it makes solving equations a lot less messy.
Example:
log3 (94)
= 4 × log3 9
= 4 × 2
= 8
Change of Base Rule
The change of base rule is super helpful when your calculator only has buttons for certain bases. It also lets you compare logs with different bases or write them in terms you prefer.
logb a = logk a / logk b
You can pick any k you like; most people use 10 or e.
Example:
log2 7 (using base 10)
= log10 7 / log10 2
≈ 0.845 / 0.301
≈ 2.81
This rule is a must when a problem gives you logs with different bases, or you need to use a calculator.
Special Logarithm Properties
Some logs show up so often that they have their own shortcut values. These are worth remembering, and you’ll spot them on lots of assignments.
- logb 1 = 0 (any base, because any number to the 0th power gives 1)
- logb b = 1 (since b to the power 1 is b)
- logb bx = x (works for any value of x)
- blogb x = x (logs and exponents cancel each other out)
Whenever you’re simplifying, these facts can help things disappear in a hurry.
How to Simplify Log Expressions
Applying log rules is all about breaking things down step by step. Here’s how I usually work through a complex log expression:
Step-by-step Example
Simplify: log3 (81 × 9)2
- Expand using the power rule:
log3 (81 × 9)2 = 2 × log3 (81 × 9) - Apply the product rule:
2 × [log3 81 + log3 9] - Evaluate each log:
log3 81 = 4 (since 34 = 81)
log3 9 = 2 (since 32 = 9) - Combine the numbers:
2 × (4 + 2) = 2 × 6 = 12
I always write out each step, since it’s easy to make mistakes if you try to do everything at once.
Here’s another quick example to practice:
Simplify log5 (125/25):
log5 125 – log5 25 = 3 – 2 = 1
Common Logarithm Mistakes and How to Fix Them
It’s really common to trip up with logs if you’re just starting. Here are a few slip-ups I’ve seen and ways to avoid them:
- Mixing up addition and multiplication:
log10 (2 + 3) does not equal log10 2 + log10 3. The rules only work for multiplying inside the log. - Forgetting the base:
Not every log is base 10! Make sure you check if it’s ln, log2, etc. - Trying to split logs over addition:
logb (M + N) cannot be split. Only products or quotients work cleanly. - Dropping parentheses:
log3 24 is not the same as (log3 2)4. Even a simple parenthesis mistake can throw off a problem.
Take it slow at first and always double-check how you’re grouping numbers and logs.
Quick Reference: Logarithm Rules TableRuleFormulaWhat It MeansProductlogb(MN) = logb M + logb NMultiplying numbers inside log splits into sumsQuotientlogb(M/N) = logb M − logb NDivision inside log becomes subtractionPowerlogb(Mp) = p × logb MTake exponents out in front as a multiplierChange of Baselogb a = logk a / logk bChange to any base you wantIdentitylogb b = 1Log base itself is always 1Zero Rulelogb 1 = 0Log of 1 is always 0
Easy Ways to Practice and Remember Log Rules
Logarithm rules stick better after you see them a few times. Here are some handy tips that helped me:
- Make your own practice problems with small numbers. Then, try solving them a few different ways using log rules.
- Write out what each rule means in plain words. For example: “A log turns multiplication into addition” pinned at the top of your page.
- Try some mental math with log rules. Recognizing that log2 32 = 5 comes up more often than you’d expect.
- When tough questions pop up, break them down. See if the product, quotient, or power rules can make the expression simpler.
The more you solve, the faster you’ll get. Over time, logs just start to feel more familiar and less intimidating.
Frequently Asked Logarithm Questions
Can any number go inside a log?
Logarithms only work for positive numbers. You can’t take the log of zero or a negative number if you’re using real numbers. If you see log10 (−5), check your math—anything negative means a step went wrong somewhere.
What’s the difference between log and ln?
“log” usually means base 10. “ln” (natural log) always means base e, which is about 2.718. The natural log shows up a ton in calculus and science problems.
How do you solve log equations?
If the variable is inside the log, try to expand or combine all log terms using product, quotient, and power rules until there’s just one log. After that, rewrite the log as an exponential equation and solve for what’s inside.
Why do logarithms even matter?
Besides showing up all over standardized tests, logs help you handle super huge or tiny numbers, tackle growth or decay questions, and crunch data in a lot of different sciences.
Next Steps and Helpful Resources
Getting a solid grip on the core log rules and knowing which one to use for each problem makes a real difference in math and beyond. If you want more practice or want to see how logs work in the real world, check out these links:
- Khan Academy’s Logarithms Course (great videos and problems)
- Purplemath: Log Rules Explanation (clear text and examples)
- Math Is Fun: Logarithms (simple visuals and review quizzes)
With these rules down and a bit of practice, log problems will seem much less stressful. You’ll spot patterns faster every time and be ready for any log challenge that comes your way!